ثـبـاح السودوكو
ولـنـواصـــل . .




بعض الحقائق عن السودوكو :

كل شبكة سودوكو مصممه بحيث هناك حل وحيد خاص لها

يقرر الإحصائيون أن هناك عدد من ألغاز السودوكو يعادل

هذا الرقم

6,670,903,752,021,072,936,960

يمكن إنتاج هذا العدد من ألغاز السودوكو !





هناك قواعد أو أشياء مساعدة بدائية يستخدمها البعض

أثناء حلـهم لألغاز السودوكو


ومنها

قاعدة الواحد فقط

وهي تعني أن أي خلية فارغة تحتمل رقما ً واحد لايمكن ملئها بغيره

قاعدة الـ 45

عندما نعمل على شبكة سودوكو من حجم 9 × 9

فإننا نعلم بديهة ً أن كل صف يجب أن يحتوي الأرقام من واحد إلى تسعة

كذلك كل عمود

كذلك كل شبكة صغرى 3 × 3

وبعبارة أخرى

فمجموع أرقام كل صف تكون خمسة وأربعين 45

كذلك مجموع أرقام كل عمود تكون 45

كذلك مجموع أرقام كل شبكة صغرى 3 × 3 تكون 45

فمتى كان المجموع أقل / أكثر من هذا نعلم أن هناك خطأ قمنا به


لكن تعالوا إلى طرق أكثر تقدما ً من هذا

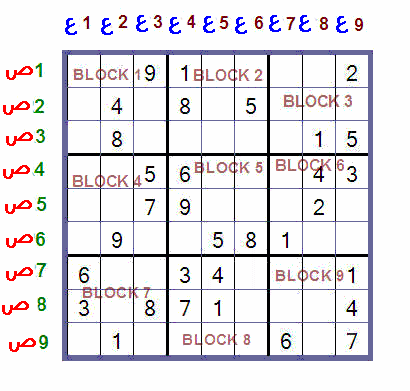
سأبدأها بطريقة بسيطه على سودوكو من المستوى السهل 9 × 9







ولغز السودوكو هذا ُمعـّـد ٌ ٌ لهذا الغرض

لأطبـِّـق عليه


فقط لنتفق على أن

ع = عمود

ص = صف

ففي الشرح مثلا ً قد أذكر ص8 / ع9 لأشير على الخلية الواقعة عند منطقة تقاطع الصف الثامن مع العمود التاسع والتي هي هنا بهذا المثال الرقم 4

وأما كلمة Block فلاشك ادركتم أنها تركز للشبكة الصغرى 3× 3

فكذلك عندما أذكر " بلوك 1 " فسأكون اشير إلى شبكة صغرى كامله هي هنا الأولى مثلا ً

أحتاج هذه الإختصارات لأنني أثناء الشرح سأذكرها هكذا ع3 مثلا ً وأعني بها العمود الثالث

وذلك لتسهيل الكتابة علي فقط

ولأنها تخدمنا - أنتم وأنا - في أغراض الشرح

أن أفضل طريقة في الغالب للمبتديء في تعلـّـم السودوكو هي أن يعمل على حل جزء من اللغز يكون هو الأسهل
وسأعمل على حل هذا اللغز بدءا ً بالرد القادم

ساترك هذه المشاركه خاصة بفهم الإرشادات

وسأبدا ً حالا ً بحل اللغز بطريقة تفصيلية مشروحه

مع بعض الإرشادات المفيدة

إنما ساحتاج لوقت

مرحى مرحى فالآن فقط استطيع ان أنطلق برشاقة

بعد ان وضعت الأساس


فلندخل هذا العالم الجمييييييييييييل
و

وللشرح بقية